
346
Chapter 8: Discrete Probability Distributions
(c) What is the probability of at least three cancellations will occur on a
particular Monday? That is, we need to find
P
(
X
3).
Solution:
(c) The time period
= 1 since the average is given as per day
and thus a Monday will represent a time period of 1 day. Also, the average
number of cancellation is
= 2 and
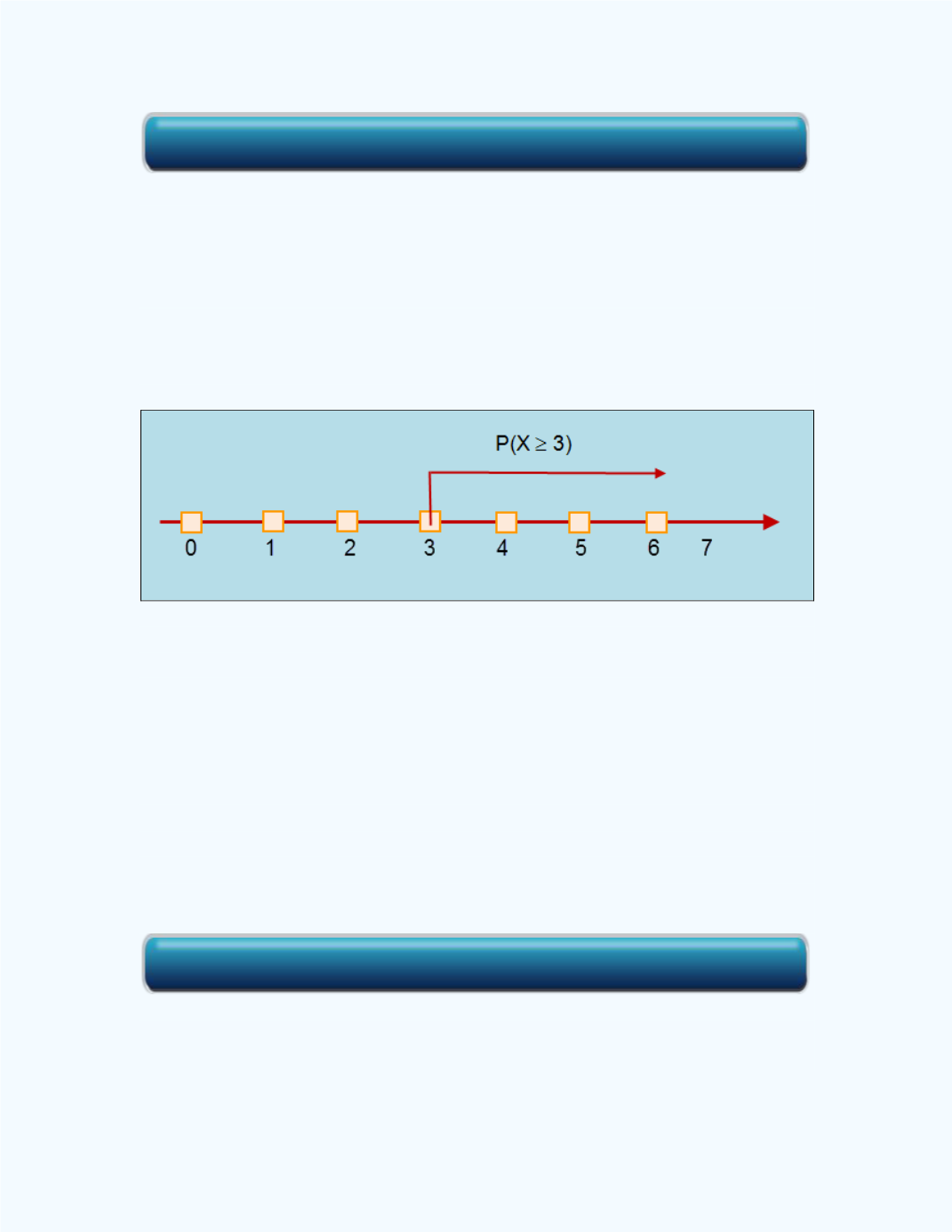
X
3. The required event is shown in
Figure 8-24
.
Figure 8-24:
Display of the event of
X
3
Since the values for the Poisson random variable can theoretically go to
infinity, it would not be wise to work this problem directly. We can use the
complement rule to help with this situation. That is, we can use the
relationship
P
(
X
3) = 1 –
P
(
X
< 3) = 1 –
P
(
X
2) = 1 – {
P
(
X
= 0)
+
P
(
X
= 1) +
P
(
X
= 2)}. Using the formula to find the individual
probabilities for
X
= 0, 1, and 2 we can show that
P
(
X
3) = 0.3233.
That is, the probability of at least three cancellations is 0.3233, correct to
four decimal places.
Figure 8-23
shows that
P
(
X
3) = 0.3233 to four
decimal places.
Click here for the Poisson Probability Distribution Workbook Click here for the Poisson Probability Distribution Workbook















