
Chapter 8: Discrete Probability Distributions
349
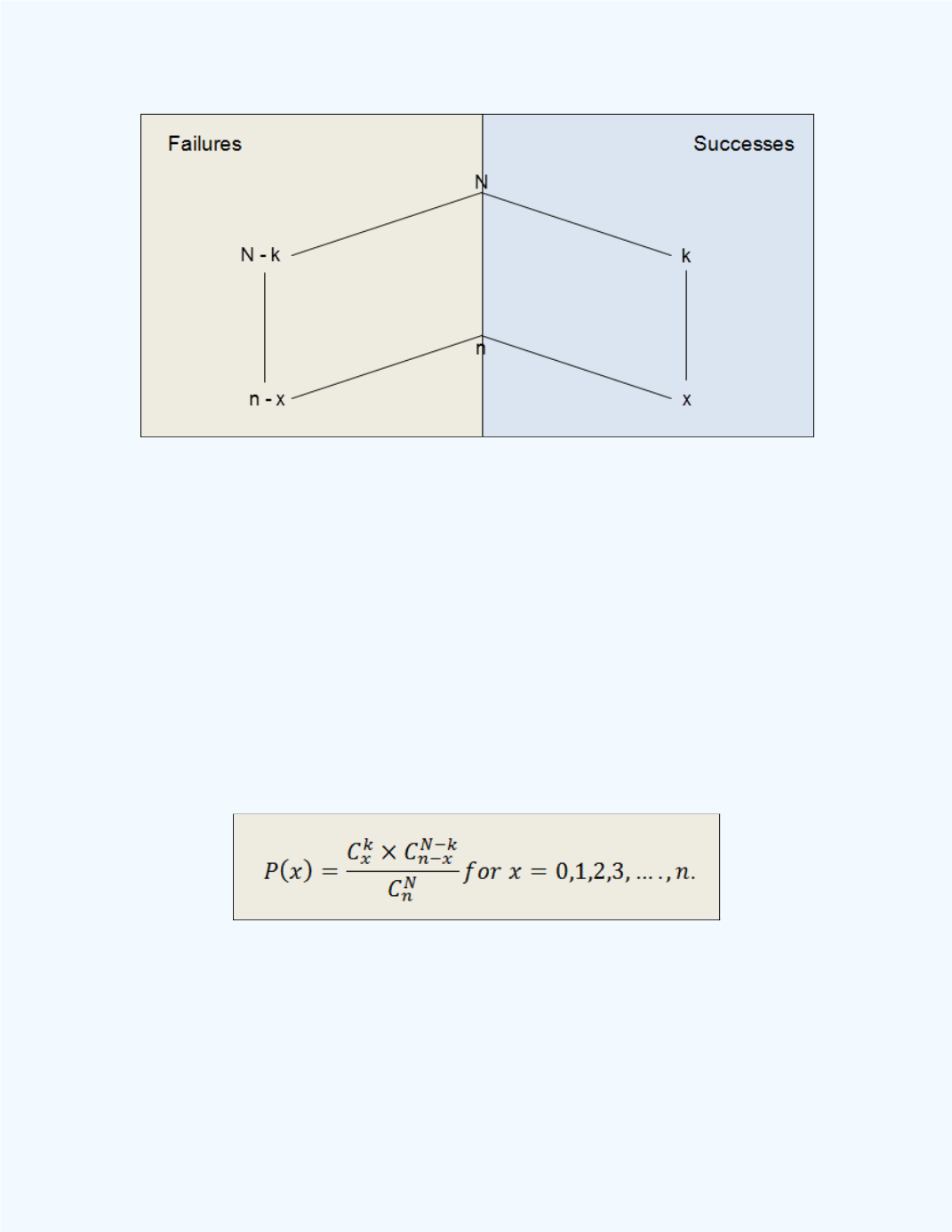
Figure 8-26:
Display of the different components used to
derive the function for theHypergeometric
Distribution
Also, from
Figure 8-26
, the number of ways of selecting a sample of size
from the population of size
will be
. Thus the probability of
selecting the
x
successes in this experiment can be obtained by dividing the
total number of ways of selecting the successes and failures by the number
of ways of selecting the sample. This will give the probability distribution
for the hypergeometric random variable
X
.
The function which generates the probability of observing the
x
success in a
hypergeometric experiment is given next.
Example 8-21
: Lots of 30 components are acceptable if they contain as
many as 2 defectives. The procedure for sampling the lot is to select 5
components at random and to reject the lot if a defective is found. What is
the probability that exactly one defective is found in the sample if there are
two defectives in the entire lot?
















