
Chapter 8: Discrete Probability Distributions
333
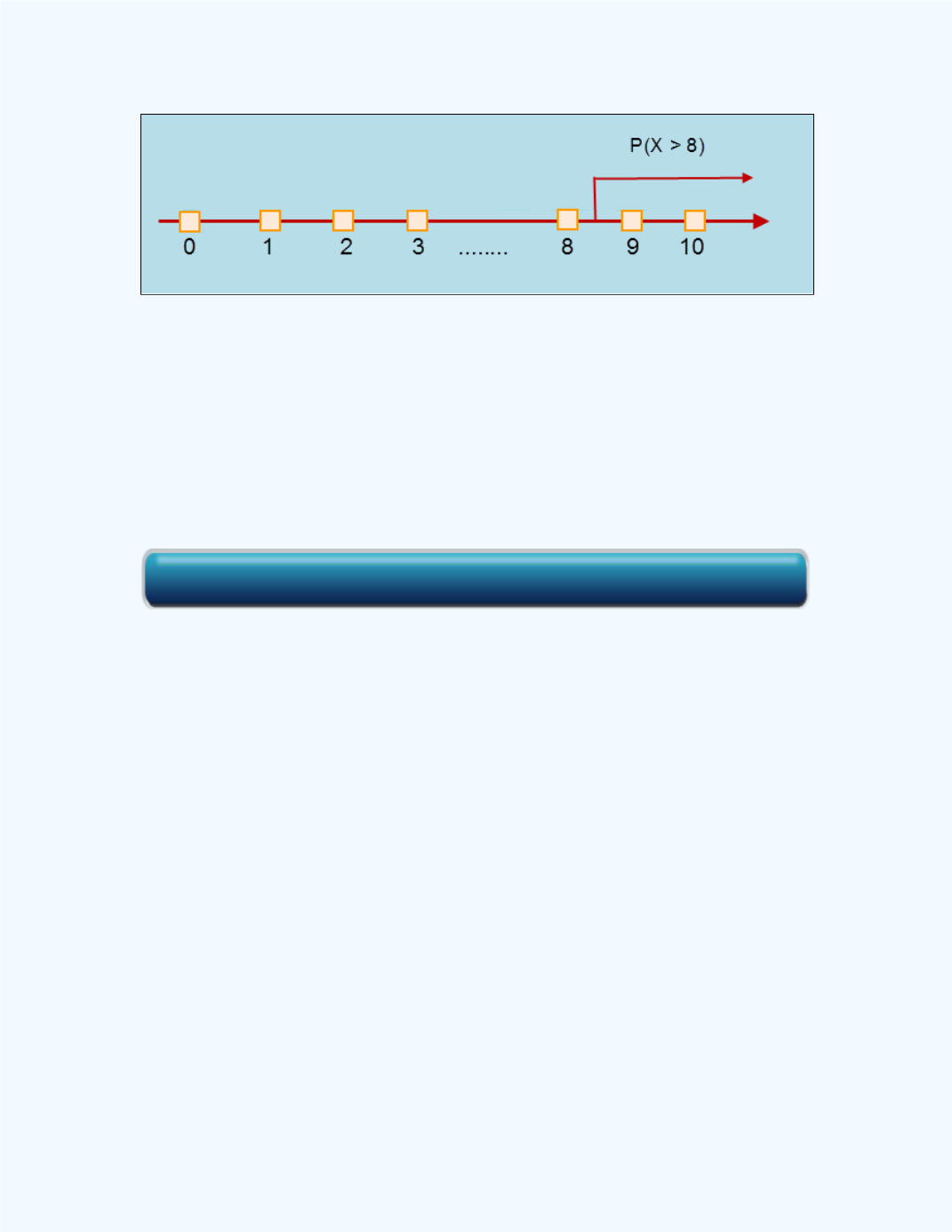
Figure 8-14:
Display of the event of
X
> 8
Now
P
(
X
> 8)
P
(
X
9) =
P
(
X
= 9 or
X
= 10) and since
X
= 9,
X
= 10 are mutually exclusive events, then
P
(
X
= 9 or
X
= 10)
=
P
(
X
= 9) +
P
(
X
= 10). Thus,
P
(
X
> 8) =
P
(
X
9) = 0.0000 + 0.0000
= 0.0000 correct to four decimal places.
From
Figure 8-12
we can also observe that
P
(
X
> 8) = 0.
Example 8-14:
A student randomly guesses at 12 multiple-choice
questions. Find the probability that the student correctly guesses
between
5
and
7 questions inclusively. Each question has four possible answers with
only one correct answer, and each question is independent of every other
question.
Solution:
Observe that this can be considered as a binomial experiment
since we have a fixed number of trials (12 questions); a fixed probability of
success (probability of guessing correctly is 0.25); the trials (questions) are
independent of each other; and there are two possible outcomes on each
question (correct guess or incorrect guess).
If we let the number of correct guesses be represented by
X
, then
X
will be a
binomial random variable with
=12,
= 0.25 and varying
values. This
situation is displayed in
Figure 8-14.
Click here for the Binomial Probability Distribution Workbook















