
Chapter 9: The Normal Probability Distribution
397
Figure 9-35:
Area and probability value for
P
(72,000
X
89,000)
Example 9-12
:
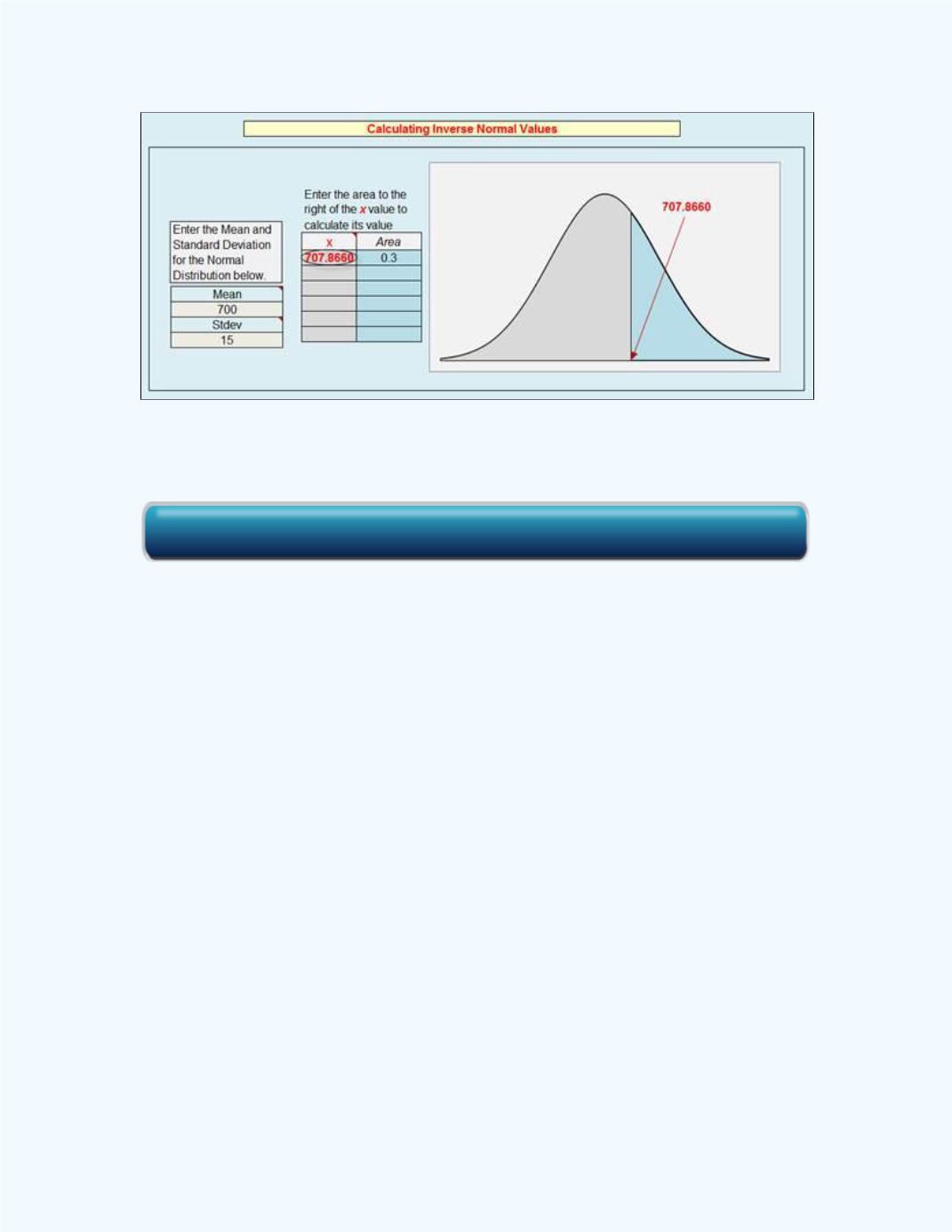
An exclusive four-year college will accept any student
ranked in the top 30 percent on a national examination. If the test scores are
normally distributed with a mean of 700 and a standard deviation of 15,
what is the cutoff score for acceptance to this exclusive college?
Solution:
In all previous problems we were asked to find probabilities.
Here we are given the probability (30%
0.3) and we are asked to find a
value. This area of 0.3 will be to the right of the required cutoff score. Thus
this is the inverse of what we have done so far in this chapter.
Let
X
= test score and let
be the cutoff score. We need to find
such
that
P
(
X
>
) = 0.3. Using the
Inverse Normal Distribution
workbook to
solve, we get
the value for
of 707.87. Thus a minimum score of
approximately 708 will be the cutoff score for acceptance. The result is
shown in
Figure 9-36
.
Click here for the Normal Probability Distribution Workbook















