
Chapter 4: Measures of Position
151
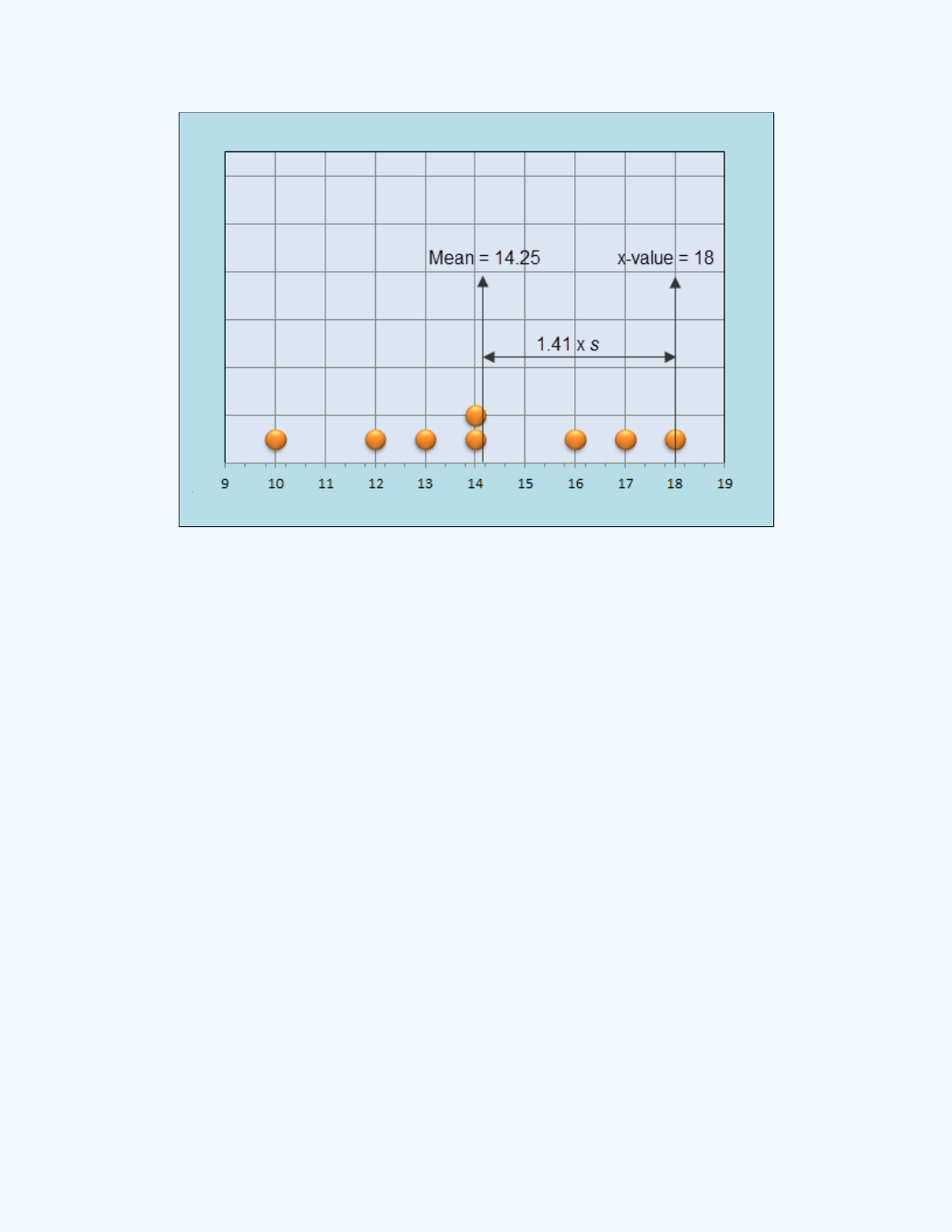
Figure 4-3:
Dot Plot of the data points with the
location of the mean and the data
value of 18 for
Example 4-1
Observe that the distance between the mean of 14.25 and the value of 18 is
approximately 1.41
= 1.41
2.6592
3.7495. Thus, if we add the mean
of 14.25 to this value of 3.7495, we will get 14.25 + 3.7495 = 17.9995
18,
the data value. This shows that the value of 18 is approximately 1.41
standard deviations
above
the mean value of 14.25.
That is, a positive
-score for a data value gives us an idea of how far the
value is above the mean, and so it gives us an idea of the position of the data
value relative to the mean.
Example 4-2:
What is the z-score for the value of 90 in the following
sample values?
96 114 100 97 101 102 99 95 90
Solution:
First, compute the sample mean and the sample standard
deviation. The sample mean
̅
= 99.3333 to four decimal places, and the
sample standard deviation,
= 6.5955 to four decimal places. We can use
















