
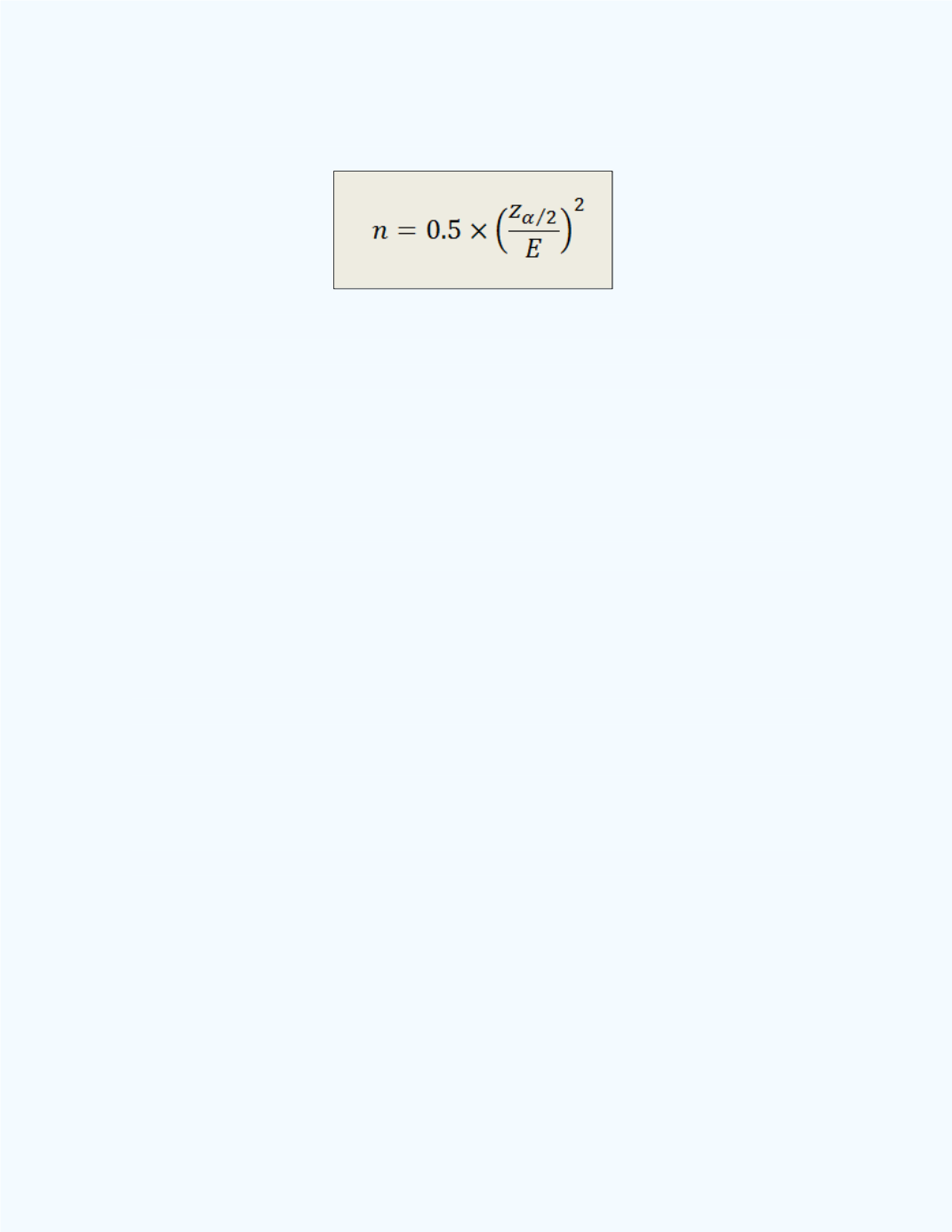
Chapter 11: Confidence Intervals – Large Samples
497
The formula needed to compute the required minimum equal sample sizes is
given next.
Note:
Again, the formula given is for when we use equal sample sizes to
obtain the estimates. When the sample sizes are not the same, the formula(s)
is (are) much more complex and will not be considered in this e-book.
Example 11-12
:
A researcher wants to determine the difference between
the proportions of males and females who are left handed. If a margin of
error of
0.01 is acceptable at the 98% confidence level, what is the
minimum sample size that should be taken?
Solution:
We are given
= 0.02 and
E
= 0.01. Since
= 0.02, then
⁄
=
2.326348 (to six decimal places).
Note:
Most tables will give a
⁄
value to two decimal places so the
computed value for
n
will be different.
Thus,
n
= 0.5
(2.326348/0.01)
2
= 27,059.47509
27,060.
That is, the researcher should sample at least 27,060 males and 27,060
females for the research study.
We can also use the
Large Sample Confidence Interval for the Difference
Between Two Population Proportions
workbook to help find the sample
sizes.
Figure 11 – 17
shows the workbook output.
















