
Chapter 11: Confidence Intervals – Large Samples
501
Example 11-13:
Two brands of similar tires were tested and their lifetimes,
in miles, were compared. Find the 95% confidence interval for the true
difference (brand A – brand B) in the means. Assume the lifetimes are
normally distributed and that the population standard deviations are known.
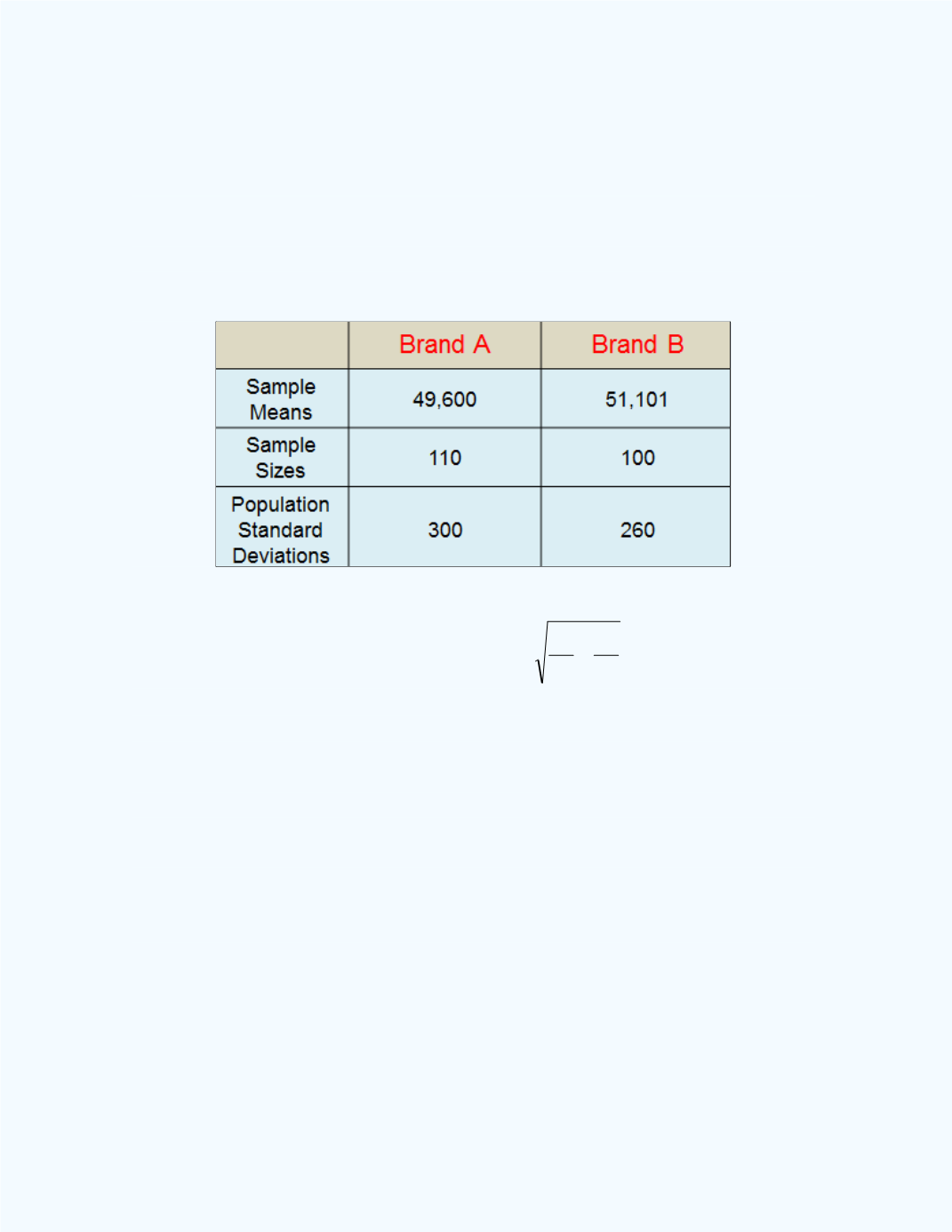
Table 11- 3
shows the results of the study.
Table 11-3:
Information Related to
Example 11-13
Solution:
From the information given, we have
= 110,
= 100,
̅
= 49,600,
̅
= 51,101,
= 300,
= 260,
2
2
2
1
2
1
σ σ
n n
= 38.654648,
= 0.05, z
/2
= 1.95996. Thus, the 95 percent confidence interval estimate
for
is (49,600 - 51,101)
1.95996
38.654648 = -1501
75.7616 (to
four decimal places). That is, we are 95 percent confident that the difference
between the means will lie between – 1576.7616 to
–1425.2384. Since both limits are negative, one may conclude that the mean
lifetime in miles for brand B is larger than the mean lifetime miles for brand
A.
We can use the
Large Sample Confidence Interval for the Difference
Between Two Population Means
workbook to help with the computations.
Figure 11 – 19
shows the workbook output.
















