
Chapter 3: Measures of Variability
135
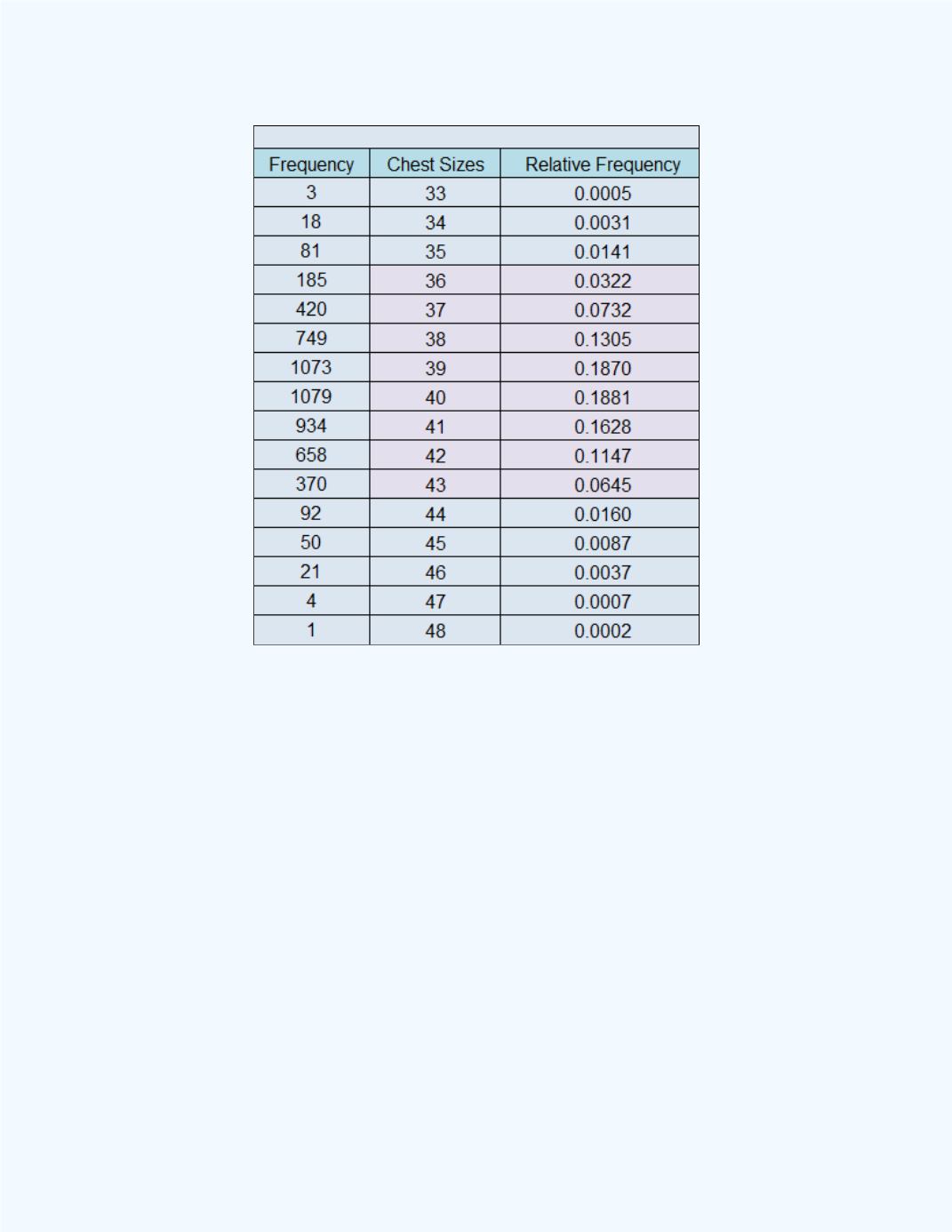
Figure 3-25:
Computed probabilities
to be included
for the Two-sigma rule for the Chest Size
data
Three Sigma Rule
Approximately 99.7 percent of the data values will lie within three standard
deviations of the mean for any bell-shaped distribution. That is, regardless
of the values for the mean and standard deviation of the distribution, the
probability that the variable will be within three standard deviations of the
mean is approximately equal to 0.997. This implies that approximately
0.3% of the values will lie outside of three standard deviations of the mean.
Thus, if we sample from a bell-shaped population we should expect about
one in every three hundred and thirty three of the values (approximately
0.3%) will lie outside three standard deviations from the mean.
Equivalently, we should expect about three hundred and thirty two out of
every three hundred and thirty three values (approximately 99.7%) will lie
















