
688
Chapter 15: Chi-Square Tests
In order to test for independence using the chi-square independence test, we
must compute expected values under the assumption that the null hypothesis
is true. To find these expected values, we need to compute the row totals
and the column totals.
These totals are called the
marginal totals
.
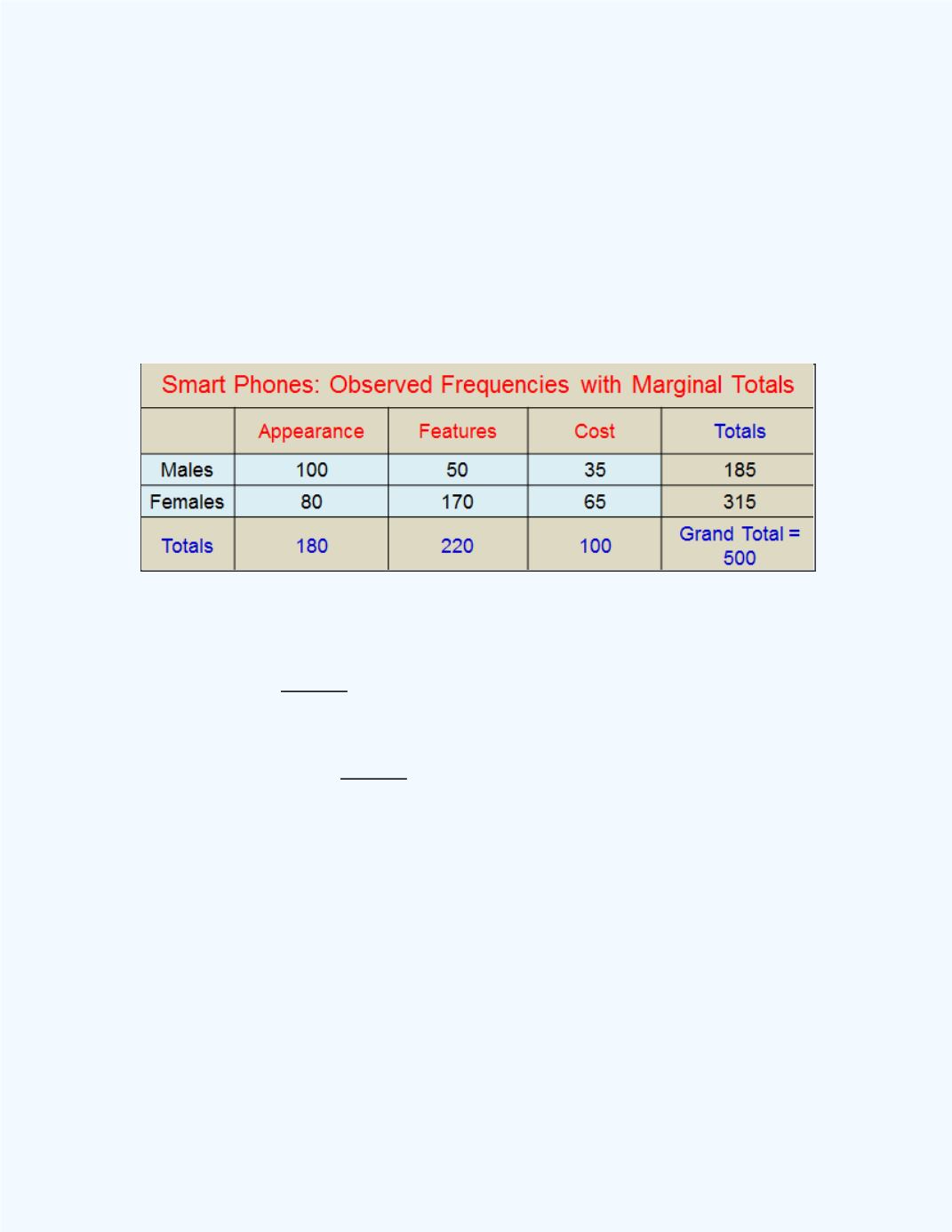
Table
15-8
shows the observed frequencies with the row and column marginal
totals.
Table 15-8:
Observed frequencieswith Marginal Totals
for
Example 15-6
For instance, the total for the first row (
Males
) is 185, and the total for the
first column (
Appearance
) is 180. The expected value for the cell in the
table where the first row (
Males
) and first column (
Appearance
) intersect
will be equal to
66.6. Recall that the grand total of the sample or
the total of the observed frequencies was 500. The expected value for the
cell corresponding to the intersection of the second row (
Females)
and the
third column (
Cost
) is
63. We can continue in this manner to
obtain the expected values for the rest of the cells in the contingency table.
Table 15-9
displays the expected frequencies for each cell in the
contingency table. Check to see that the entries are correct.
















