
318
Chapter 8: Discrete Probability Distributions
That is, if you purchase a large number of tickets, on average, the return on
each ticket will be $0.9. Thus, it would be unwise to spend more than $0.9
for a ticket.
Example 8-4:
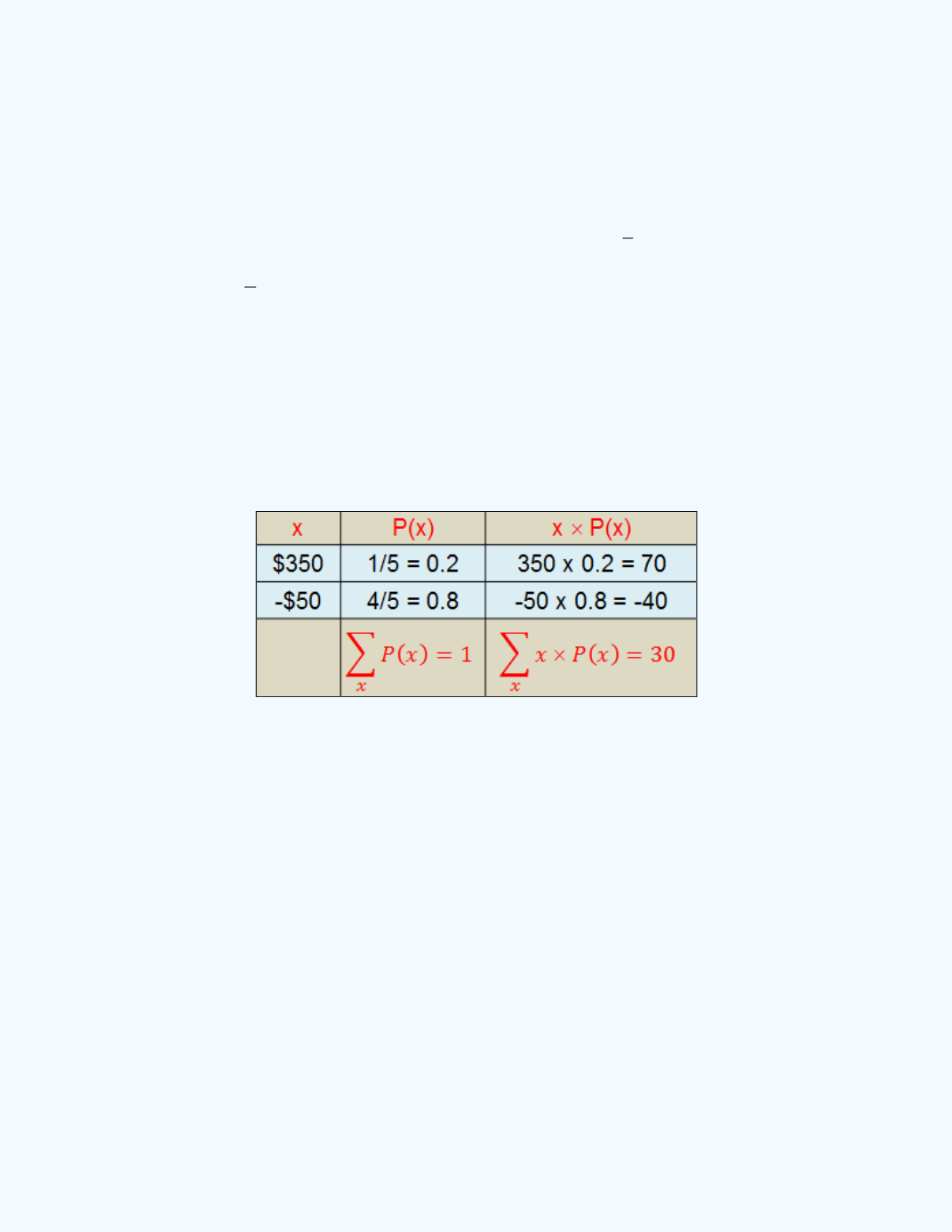
A game is set up such that you have a
5
1
chance of winning
$350 and a
5
4
chance of losing $50. What is your expected gain?
Solution:
Let the amount of gain be represented by the random variable
X
.
Note, a loss will be considered as a negative gain. The probability
distribution for
X
and the necessary computations are given in
Table 8-7
.
Table 8-7:
Probability distribution for
Example 8-4
Thus, the expected value of the game is
E
(
X
) = $30. That is, if you play the
game a large number of times, on average, you will win $30 per game.
Sometimes we may be able to use expected values to help make a decision.
The following example illustrates this.
Example 8-5:
Suppose you are given the option of two investment
portfolios, A and B, with potential profits and the associated probabilities
displayed in
Table 8-8
. Based on expected profits, which portfolio will you
choose?
















