
316
Chapter 8: Discrete Probability Distributions
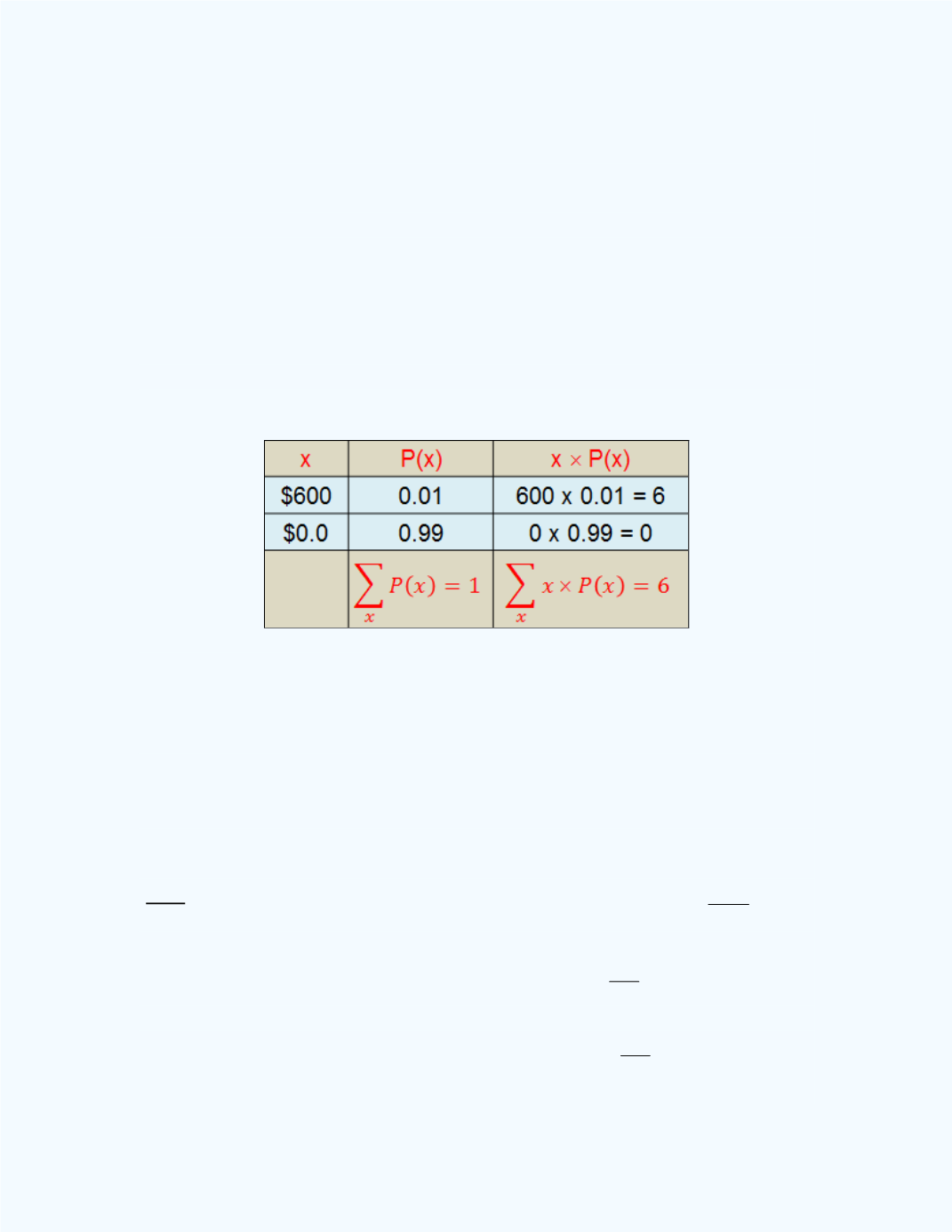
Example 8-2:
If 100 raffle tickets were sold for a tablet computer worth
$600, and a ticket number is drawn at random to determine the winner, what
is the expected value of the raffle?
Solution:
The probability of winning the tablet is 1/100 = 0.01, since there
were 100 raffle tickets and the ticket number is drawn at random. Also, the
probability of not winning the tablet is 99/100 = 0.99.
Table 8-4
shows the
necessary computations for this example. Thus the expected value of the
raffle will be $600
0.01 + $0.00
0.99 = $6.
Table 8-4:
Table showing the Probability
Distribution and Expected value computations
for
Example 8-2
That is, if you purchase a large number of tickets, on average, the return on
each ticket will be $6. Thus, it would be unwise to spend more than $6 for a
ticket.
Example 8-3:
What is the expected value of a raffle with a first prize of
$500, a second prize of $300, and a third prize of $100 if 1,000 tickets are
sold?
Solution:
If the raffle was repeated a large number of times, we will lose
of the time. We will win the first prize
100
000 ,1
1
percent = 0.1 percent of the time, since initially there will be 1,000 tickets
from which to choose. We will win the second prize
100
999
1
percent = 0.1
percent of the time, since we only will have 999 remaining tickets to choose
from for the second prize. We will win the third prize
100
998
1
percent = 0.1
percent of the time, since we only have 998 remaining tickets from which to
















