
252
Chapter 6: Categorical Data
6-4 Independence in Categorical Variables
Sometimes it is important to determine whether there is an association
between the variables in a contingency table; that is, whether the variables
are independent or dependent. This concept will be discussed further in
Chapter 15
. In this chapter, we will use the concept of conditional
distributions for contingency tables to determine whether there is an
association between the variables.
What do we mean by the independence between two categorical variables?
Definition: Independence in Categorical Variables
Two categorical variables are said to be independent of each other (have no
association) if the conditional distributions of one variable are the same for
every category of the other variable.
Example 6-8:
A faculty member conducted a survey on a college campus
to determine the favorability rating of the college president. One hundred
randomly selected students were asked to indicate whether they view the
president favorably or unfavorably.
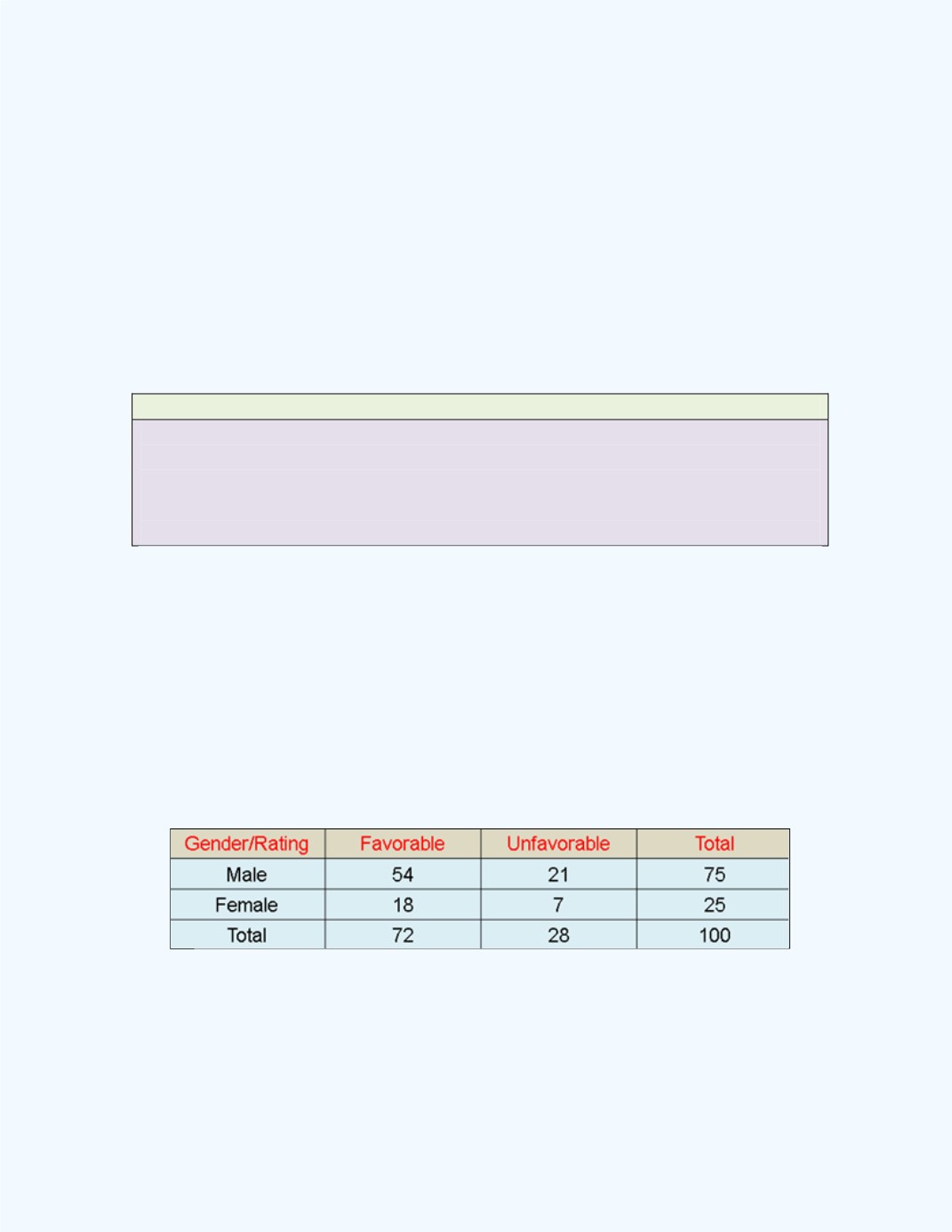
Table 6-7
shows a 2
2 contingency
table summarizing the results for both male and female students in the
sample.
Table 6-7:
Favorability Rating of the College President
by Gender
(a) Construct a table of the conditional distributions for the gender
classification given the favorable/unfavorable ratings of the college
president.
















